TEOREMAS DE CIRCUITOS ELÉCTRICOS 
Ley de Ohm.
La ley de Ohm, postulada por el físico y matemático alemán Georg Simon Ohm, es una ley básica de la electricidad. Establece que la intensidad de la corriente  que circula por un conductor es proporcional a la diferencia de potencial
que circula por un conductor es proporcional a la diferencia de potencial  que aparece entre los extremos del citado conductor. Ohm completó la ley introduciendo la noción de resistencia eléctrica
que aparece entre los extremos del citado conductor. Ohm completó la ley introduciendo la noción de resistencia eléctrica  ; esta es el coeficiente de proporcionalidad que aparece en la relación entre
; esta es el coeficiente de proporcionalidad que aparece en la relación entre  y
y  :
:
 que circula por un conductor es proporcional a la diferencia de potencial
que circula por un conductor es proporcional a la diferencia de potencial  que aparece entre los extremos del citado conductor. Ohm completó la ley introduciendo la noción de resistencia eléctrica
que aparece entre los extremos del citado conductor. Ohm completó la ley introduciendo la noción de resistencia eléctrica  ; esta es el coeficiente de proporcionalidad que aparece en la relación entre
; esta es el coeficiente de proporcionalidad que aparece en la relación entre  y
y  :
:
Georg Simon Ohm
En la fórmula,  corresponde a la intensidad de la corriente,
corresponde a la intensidad de la corriente,  a la diferencia de potencial y
a la diferencia de potencial y  a la resistencia. Las unidades que corresponden a estas tres magnitudes en el sistema internacional de unidades son, respectivamente,amperios (A), voltios (V) y ohmios (Ω).
a la resistencia. Las unidades que corresponden a estas tres magnitudes en el sistema internacional de unidades son, respectivamente,amperios (A), voltios (V) y ohmios (Ω).
 corresponde a la intensidad de la corriente,
corresponde a la intensidad de la corriente,  a la diferencia de potencial y
a la diferencia de potencial y  a la resistencia. Las unidades que corresponden a estas tres magnitudes en el sistema internacional de unidades son, respectivamente,amperios (A), voltios (V) y ohmios (Ω).
a la resistencia. Las unidades que corresponden a estas tres magnitudes en el sistema internacional de unidades son, respectivamente,amperios (A), voltios (V) y ohmios (Ω).
Leyes de Kirchhoff
son dos igualdades que se basan en la conservación de la energía y la carga en los circuitos eléctricos. Fueron descritas por primera vez en 1845 por Gustav Kirchhoff. Son ampliamente usadas en ingeniería eléctrica.
Ambas leyes de circuitos pueden derivarse directamente de las ecuaciones de Maxwell, pero Kirchhoff precedió a Maxwell y gracias a Georg Ohm su trabajo fue generalizado. Estas leyes son muy utilizadas en ingeniería eléctrica e ingeniería eléctronica para hallar corrientes y tensiones en cualquier punto de un circuito eléctrico.
Ley de Corrientes de Kirchhoff
Esta ley también es llamada ley de nodos o primera ley de Kirchhoff y es común que se use la sigla LCK para referirse a esta ley. La ley de corrientes de Kirchhoff nos dice que:
|
Esta fórmula es válida también para circuitos complejos:
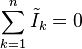
La ley se basa en el principio de la conservación de la carga donde la carga en couloumbs es el producto de la corriente en amperios y el tiempo en segundos.
Ley de tensiones de kirchhoff
Esta ley es llamada también Segunda ley de Kirchhoff, ley de lazos de Kirchhoff o ley de mallas de Kirchhoff y es común que se use la sigla LVKpara referirse a esta ley.
|
De igual manera que con la corriente, los voltajes también pueden ser complejos, así:
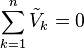
Ley de tensiones de Kirchhoff, en este caso v4= v1+v2+v3. No se tiene en cuenta a v5 porque no forma parte de la malla que estamos analizando.
Gustav Kirchhoff
Teorema de Kennely
El teorema de Kennelly, llamado así en homenaje a Arthur Edwin Kennelly, permite determinar la carga equivalente en estrella a una dada en triángulo y viceversa. El teorema también se le suele llamar de transformación estrella-triángulo(escrito Y-Δ) o transformación te-delta (escrito T-Δ).
En la siguiente tabla se muestran las ecuaciones de transformación en función de las impedancias y de las admitancias.
Ecuaciones de Kennelly
Transformación Δ-Y
En función de las impedancias en funcion de las admitancias


Transformación Y-Δ
En función de las impedancias en funcion de las admitancias


DEMOSTRACIÓN
A continuación se demuestra analíticamente las ecuaciones de Kennelly.
Circuito Triángulo a estrella[editar]
Supongamos conocidos los valores ZAB, ZBC y ZAC de la carga en triángulo de la figura 1 y deseamos obtener los valores ZAT, ZBT y ZCT de su equivalente en estrella. Para ello obtendremos en ambos circuitos las impedancias equivalentes respecto de los puntos A-B, B-C y A-C y las igualaremos puesto que son cargas equivalentes (observe que en la estrella quedan siempre dos impedancias en serie, mientras que en el triángulo quedan dos en serie con la tercera en paralelo):



La ecuaciones de Kennelly se obtienen a partir de las anteriores del siguiente modo:
- Sumando las ecuaciones (1) y (3) y restando el resultado de la (2)
- Sumando las ecuaciones (1) y (2) y restando el resultado de la (3)
- Sumando las ecuaciones (2) y (3) y restando el resultado de la (1)
Estrella a triángulo[editar]
Supongamos ahora el caso opuesto, esto es, conocidos los valores ZAT, ZBT y ZCT de la estrella de la figura 1, deseamos obtener los valores ZAB, ZBC y ZAC de la carga en triángulo equivalente. Para ello se tomarán las ecuaciones de transformación Δ-Y, donde por simplificación de notación tomaremos

quedando las ecuaciones siguientes:
 ; ; |  ; ; |  |
Realizando las tres multiplicaciones binarias posibles entre ellas, se obtiene



Y sumándolas


Dividamos el primer miembro por el valor de
 :
:

Y dividiendo el segundo miembro por
 :
:
Igualando ambos resultados obtenemos una de las ecuaciones de transformación. Las otras dos pueden obtenerse del mismo modo dividiendo por
 y
y 
TEOREMA DE NORTON
El teorema de Norton para circuitos eléctricos es dual del teorema de Thévenin. Se conoce así en honor al ingeniero Edward Lawry Norton, de los Laboratorios Bell, que lo publicó en un informe interno en el año 1926.1 El alemán Hans Ferdinand Mayer llegó a la misma conclusión de forma simultánea e independiente.
Establece que cualquier circuito lineal se puede sustituir por una fuente equivalente de intensidad en paralelo con una impedancia equivalente.
Al sustituir un generador de corriente por uno de tensión, el borne positivo del generador de tensión deberá coincidir con el borne positivo del generador de corriente y viceversa.
Una caja negra que contiene exclusivamente fuentes de tensión, fuentes de corriente y resistencias puede ser sustituida por un circuito Norton equivalente.
CALCULO DEL CIRCUITO NORTON EQUIVALENTE
 El circuito Norton equivalente consiste en una fuente de corriente INo en paralelo con una resistencia RNo. Para calcularlo:
El circuito Norton equivalente consiste en una fuente de corriente INo en paralelo con una resistencia RNo. Para calcularlo:- Se calcula la corriente de salida, IAB, cuando se cortocircuita la salida, es decir, cuando se pone una carga (tensión) nula entre A y B. Al colocar un cortocircuito entre A y B toda la intensidad INo circula por la rama AB, por lo que ahora IAB es igual a INo.
- Se calcula la tensión de salida, VAB, cuando no se conecta ninguna carga externa, es decir, cuando se pone una resistencia infinita entre A y B. RNo es ahora igual a VAB dividido entre INo porque toda la intensidad INo ahora circula a través de RNo y las tensiones de ambas ramas tienen que coincidir ( VAB = INoRNo ).
CIRCUITO THEVENIN EQUIVALENTE A UN CIRCUITO NORTON
Para analizar la equivalencia entre un circuito Thévenin y un circuito Norton pueden utilizarse las siguientes ecuaciones:
Paso 1: El circuito original Paso 2: Calculando la intensidad de salida equivalente al circuito actual
Paso 3: Calculando la resistencia equivalente al circuito actual

En el ejemplo, Itotal viene dado por:

Usando la regla del divisor, la intensidad de corriente eléctrica tiene que ser:


Y la resistencia Norton equivalente sería:

Por lo tanto, el circuito equivalente consiste en una fuente de intensidad de 3.75mA en paralelo con una resistencia de 2 kΩ
Teorema de superposición
El teorema de superposición sólo se puede utilizar en el caso de circuitos eléctricos lineales, es decir circuitos formados únicamente por componentes lineales (en los cuales la amplitud de la corriente que los atraviesa es proporcional a la amplitud de voltaje a sus extremidades).
El teorema de superposición ayuda a encontrar:
- Valores de voltaje, en una posición de un circuito, que tiene más de una fuente de voltaje.
- Valores de corriente, en un circuito con más de una fuente de voltaje.
Este teorema establece que el efecto que dos o más fuentes tienen sobre una impedancia es igual, a la suma de cada uno de los efectos de cada fuente tomados por separado, sustituyendo todas las fuentes de voltaje restantes por un corto circuito, y todas las fuentes de corriente restantes por un circuito abierto.
Por ejemplo, si el voltaje total de un circuito dependiese de dos fuentes de tensión:

INTERÉS DEL TEOREMA
En principio, el teorema de superposición puede utilizarse para calcular circuitos haciendo cálculos parciales, como hemos hecho en el ejemplo precedente. Pero eso no presenta ningún interés práctico porque la aplicación del teorema alarga los cálculos en lugar de simplificarlos. Hay que hacer un cálculo separado por cada fuente de voltaje y de corriente y el hecho de eliminar los otros generadores no simplifica mucho o nada el circuito total. Otros métodos de cálculo son mucho más útiles.
El verdadero interés del teorema de superposición es teórico. El teorema justifica métodos de trabajo con circuitos que simplifican verdaderamente los cálculos. Por ejemplo, justifica que se hagan separadamente los cálculos de corriente continua y los cálculos de señales (corriente alterna) en circuitos con Componentes activos (transistores, amplificadores operacionales, etc.).
Otro método justificado por el teorema de superposición es el de la descomposición de una señal no sinusoidal en suma de señales sinusoidales (ver descomposición en serie de Fourier). Se reemplaza un generador de voltaje o de corriente por un conjunto (tal vez infinito) de fuentes de voltaje en serie o de fuentes de corriente en paralelo. Cada una de las fuentes corresponde a una de las frecuencias de la descomposición. Por supuesto no se hará un cálculo separado para cada una de las frecuencias, sino un cálculo único con la frecuencia en forma literal. El resultado final será la suma de los resultados obtenidos remplazando, en el cálculo único, la frecuencia por cada una de las frecuencias de la serie de Fourier. El enorme interés de esto es el de poder utilizar el cálculo con el formalismo de impedancias cuando las señales no son sinusoidales.
El verdadero interés del teorema de superposición es teórico. El teorema justifica métodos de trabajo con circuitos que simplifican verdaderamente los cálculos. Por ejemplo, justifica que se hagan separadamente los cálculos de corriente continua y los cálculos de señales (corriente alterna) en circuitos con Componentes activos (transistores, amplificadores operacionales, etc.).
Otro método justificado por el teorema de superposición es el de la descomposición de una señal no sinusoidal en suma de señales sinusoidales (ver descomposición en serie de Fourier). Se reemplaza un generador de voltaje o de corriente por un conjunto (tal vez infinito) de fuentes de voltaje en serie o de fuentes de corriente en paralelo. Cada una de las fuentes corresponde a una de las frecuencias de la descomposición. Por supuesto no se hará un cálculo separado para cada una de las frecuencias, sino un cálculo único con la frecuencia en forma literal. El resultado final será la suma de los resultados obtenidos remplazando, en el cálculo único, la frecuencia por cada una de las frecuencias de la serie de Fourier. El enorme interés de esto es el de poder utilizar el cálculo con el formalismo de impedancias cuando las señales no son sinusoidales.
EJEMPLO
En el circuito de arriba de la figura de la izquierda, calculemos el voltaje en el punto A utilizando el teorema de superposición.Como hay dos generadores, hay que hacer dos cálculos intermedios.
En el primer cálculo, conservamos la fuente de voltaje de la izquierda y remplazamos la fuente de corriente por un circuito abierto. El voltaje parcial obtenido es::
En el segundo cálculo, guardamos la fuente de corriente de derecha y remplazamos la fuente de voltaje por un cortocircuito. El voltaje obtenido es::
.El voltaje que buscamos es la suma de los dos voltajes parciales::
Arriba:circuito original.
En medio: circuito con sólo la fuente de voltaje.
Abajo:circuito con sólo la fuente de corriente.
Análisis de Circuito
Un circuito eléctrico es un grupo de componentes interconectados. El análisis de circuitos es el proceso de calcular intensidades, tensiones o potencias. Existen muchas técnicas para lograrlo, Sin embargo, se asume que los componentes de los circuitos son lineales. Los métodos descritos en este artículo solo se aplican al análisis de circuitos lineales salvo en los casos expresamente establecidos. Para entender este artículo se necesitan saber las partes básicas de un circuito así como sus leyes fundamentales.
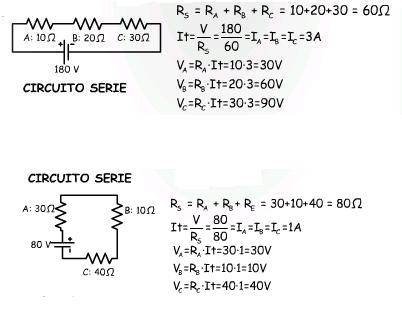
explicación Ejercicio por la le de ohm
Ejercicios Resueltos



En el primer cálculo, conservamos la fuente de voltaje de la izquierda y remplazamos la fuente de corriente por un circuito abierto. El voltaje parcial obtenido es::

En el segundo cálculo, guardamos la fuente de corriente de derecha y remplazamos la fuente de voltaje por un cortocircuito. El voltaje obtenido es::

.El voltaje que buscamos es la suma de los dos voltajes parciales::

Arriba:circuito original.
En medio: circuito con sólo la fuente de voltaje.
Abajo:circuito con sólo la fuente de corriente.
Análisis de Circuito
Un circuito eléctrico es un grupo de componentes interconectados. El análisis de circuitos es el proceso de calcular intensidades, tensiones o potencias. Existen muchas técnicas para lograrlo, Sin embargo, se asume que los componentes de los circuitos son lineales. Los métodos descritos en este artículo solo se aplican al análisis de circuitos lineales salvo en los casos expresamente establecidos. Para entender este artículo se necesitan saber las partes básicas de un circuito así como sus leyes fundamentales.
DEFINICIONES BÁSICAS, PARTES DE UN CIRCUITO
| Componente | Un dispositivo con dos o más terminales capaz de hacer fluir carga. |
| Nodo | Punto donde dos o más elementos tienen una conexión común. Se considera un nodo a un conductor con una resistencia igual a cero. |
| Rama | Una rama es un conjunto de elementos que se pueden simplificar formando un dispositivo que represente el comportamiento de ellos. |
| Malla | Cualquier circuito cerrado de ramas es una malla, con la condición que no pase dos veces por el mismo nodo. |
| Circuito | Red donde circula una corriente proveniente de una fuente, a través de componentes pasivos. Un circuito es, en este sentido, una red de dos terminales que sea trivial analizarse. Frecuentemente, "circuito" y "red" se usan indistintamente, pero muchos analistas reservan "red" para referirse a un modelo idealizado consistente de componentes ideales.1 |
| Función de transferencia | La relación de las corrientes y tensiones de dos puertos. Se define frecuentemente como una comparación entre un puerto de entrada y un puerto de salida para determinar ganancia o atenuación. explicación de ejercicios por la ley de kirchhoff |
explicación Ejercicio por la le de ohm
Ejercicios Resueltos



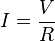






















Best Casinos and Gambling Sites Near Harris, TX
ResponderEliminarFind the best casinos and 동두천 출장안마 gambling sites 전라남도 출장안마 in Harris, TX. Explore reviews, 여수 출장마사지 photos and maps to 상주 출장마사지 find the best casino and gambling 김해 출장마사지 sites.